Limite de la fusion stéréoscopique
Lorsque nous fixons un sujet éloigné, et que l’on place un deuxième objet à une distance beaucoup plus proche, nous le voyons dédoublé (diplopie croisée). De la même manière, si nous fixons un sujet proche, les sujets lointains nous apparaîtrons également dédoublé (diplopie homonyme). Dans les deux cas, le cerveau ne parvient pas à fusionner une partie de l’image car elles sont trop séparées sur le plan horizontal.
Panum démontra en 1850 que la limite de fusion stéréoscopique (limite de Panum) est d’environ 1° (valeur constamment dépassée dans les conditions normales de la vision).
Application à l’image stéréoscopique
Plusieurs théories existent concernant les limitations sur la différence de distance entre le sujet le plus proche et le plus éloigné. Nous en présentons deux ci-dessous de manière courte.
Dans tous les cas, il est important de noter des facteurs comme la composition de l’image, la taille de l’écran, la luminosité jouent un rôle majeur pour guider le regard du spectateur dans la profondeur. La notion de confort évoquée ici est donc très relative. Nous avons remarqué qu’une image avec de grandes différences de profondeur peut être tout à fait lisible selon sa nature.
Règle de Lipton
Dans son étude intitulée “Composition for Electrostereoscopic Displays”, Lipton, se basant sur les recherches effectuées sur l’aire de Panum, conclue que l’angle α formé par deux droites reliant le point le plus loin et le point le plus proche doit être compris entre -1.5° et +1.5° (voir dessin ci-dessous). Il intitule ce paramètre Binocular disparity threshold ou BDT ou seuil de disparité binoculaire.
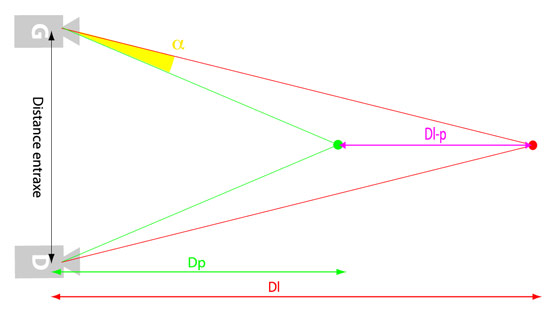
L’animation ci-dessous nous montre de quelle manière le seuil de disparité occulaire (angle α) varie en fonction de la profondeur du sujet de la distance entraxe.
Une formule trigonométrique nous permet de calculer cet angle en fonction de ces paramètres.
α= ATAN (2*distance lointain/distance entraxe) – ATAN (2*distance premier plan/distance entraxe)
Nous basant sur cette théorie, avons mis au point un petit tableau utilisable en tournage (télécharger ici)
.
.
Règle d’Olivier Cahen
Dans son livre, Olivier Cahen conclue que le spectateur ne peut voir confortablement en relief à la fois des objets éloignés et des objets proches que si la différence de proximité entre ces objets vus l’un contre l’autre ne dépasse pas un certain seuil.
Olivier Cahen cite dans son livre les valeurs limites de différence de proximité définies par Maillard (valable uniquement si l’on travaille sans anguler les caméras!):
- Limite absolue pour des plans disjoints: 0.8 à 1.2 ertems

les plans sont disjoints (ne se cachent pas l'un l'autre)
…
- Limite si les objets sont contigus: 0.3 ertems

les plans sont contigus (se cachent l'un l'autre)
..
La différence de proximité (exprimée ici en ertems) se calcul de la manière suivante : (1/p-1/q)
p = distance 1er plan (en m)
q= distance des fonds (en m)
